 ISSN: 2710-088X - ISSN-L: 2710-088X
ISSN: 2710-088X - ISSN-L: 2710-088X
Volumen 6,
No. 16 / Mayo - agosto 2024
Páginas 43 -
79

“La granja matemática” herramienta didáctica para
solución de situaciones problema. Uso de estructuras aditivas -multiplicativas.
“The mathematical farm” didactic tool for solving problem situations.
Use of additive-multiplicative structures
Yenny
Giraldo Martínez
yennygiraldom@gmail.com
https://orcid.org/0000-0002-6192-7577
Institución
Educativa La Magdalena, Buga, Colombia
Julián
Andrés Montoya Jiménez
Jam85722@gmail.com
https://orcid.org/0000-0003-4023-4912
Institución
Educativa La Magdalena, Buga, Colombia
Artículo recibido 30
de enero 2024 / arbitrado 03 de marzo 2024 / aceptado 30 de marzo 2024 /
publicado 02 de mayo 2024
DOI: https://doi.org/10.61287/revistafranztamayo.v.6i16.10
Resumen
Este ejercicio de investigación se origina
del análisis de resultados alcanzados por los educandos en pruebas de carácter
institucional y nacional (Evaluar para Avanzar, pruebas SABER). La poca
escolarización de las familias, las creencias culturales, la falta de afinidad
con las matemáticas y el papel que asumen los docentes de matemáticas impactan
de manera negativa y determinante sobre estas. Con el estudio y apropiación de
las estructuras aditivas y multiplicativas aplicadas al contexto en el que se
inscriben los niños se logra un cambio positivo en el cambio de paradigma. Con
esta orientación se propuso un proyecto, que responde a los objetivos de la
Investigación Acción, con la implementación de secuencias didácticas, cuyo eje
central son las estructuras aditivas y multiplicativas en situaciones problema
aplicadas en el contexto. Enfoque que promovió la dinamización del ejercicio
hasta lograr resultados satisfactorios entre lo teórico, lo práctico y lo
contextual de las matemáticas.
Palabras
clave:
Competencias; Didáctica; Situación Problema; Estructuras aditivas; Estructuras
multiplicativas.
Abstract
This research exercise originates from the
analysis of results achieved by students in institutional and national tests
(Evaluate to Advance, SABER tests). The little schooling of families, cultural
beliefs, lack of affinity with mathematics and the role that mathematics
teachers assume have a negative and decisive impact on them. With the study and
appropriation of additive and multiplicative structures applied to the context
in which children are enrolled, a positive change is achieved in the paradigm
shift. With this orientation, a project was proposed, which responds to the
objectives of Action Research, with the implementation of didactic sequences,
whose central axis are additive and multiplicative structures in problem
situations applied in the context. Approach that promoted the dynamization of
the exercise until satisfactory results were achieved between the theoretical,
practical and contextual aspects of mathematics.
Keywords: Competencies;
Didactics; Problem situation; Additive structures; Multiplicative structures.
INTRODUCCIÓN
El presente artículo es el producto del
proyecto de intervención “La granja matemática” herramienta didáctica para
solución de situaciones problema. Uso de estructuras
aditivas -multiplicativas”
que se aplicó con los estudiantes de básica primaria (4° y 5°) de la
Institución Educativa La Magdalena (sede Marco Fidel Suárez) del municipio
Guadalajara de Buga. Este proyecto pretende mejorar la comprensión y aplicación
de las estructuras aditivas y multiplicativas en la solución de situaciones problema enmarcados en el pensamiento numérico, con el
objetivo de mitigar los resultados desfavorables presentados por los
estudiantes en el área de matemáticas según los indicadores extraídos de los
últimos informes en las evaluaciones nacionales (Evaluar Para Avanzar y Pruebas
Saber).
Como punto de partida, se exponen las
problemáticas que movilizaron el diseño y la realización del proyecto.
Seguidamente se presenta una caracterización del contexto de la población local
e institucional que participan de este. También, se dan argumentos sólidos que
justifican el para qué y el porqué de este ejercicio de investigación. Por
último, se enuncian los objetivos que se espera alcanzar al finalizar la
intervención que se desprende de este ejercicio de investigación.
Dentro de la fundamentación teórica y
conceptual que orientó tanto la formulación del proyecto como su ejecución,
inicialmente se presenta una recopilación de las matemáticas y sus primeras
apariciones desde (Gutiérrez, 2009) y la evolución de las mismas en la historia
de la humanidad sustentada por (Loyes, 1993). Seguidamente se presenta una
definición aportada por (Wilson et al, 2006) de lo que se entiende por
competencia matemática, así como también se relaciona la concepción de la misma
en el marco del proyecto PISA (Rico, 2006), del mismo modo se señalan las
habilidades implícitas en el dominio de la competencia matemática señaladas por
(Leyva y Proenza,2006). Se argumenta desde la postura
de (Lovell, 1962) y (Castro,2004) las diferentes
etapas que se presentan entre los niños y el desarrollo del conocimiento matemático.
Un aspecto importante de este segmento es el papel que juegan las creencias y
que son de carácter cultural en el aprendizaje de las matemáticas, dichas
creencias tienen su origen en malas experiencias pasadas y hasta se sustentan
desde la genética (Vila y Callejo, 2004).
Los referentes de orden disciplinar se
ubicaron desde los aportes de (Castro, Rico y Castro 1995) que sustentan la
base teórica de las estructuras aditivas y multiplicativas donde se explica
cada estructura y su modelación. Del mismo modo que se toman las referencias
del Ministerio de Educación Nacional (MEN, 2006) y la perspectiva de (Santos,2007) en torno a la importancia de la solución de problemas
como estrategia didáctica.
Seguidamente, se sustentan los referentes que
orientaron la línea metodológica y que definen la ruta de intervención y la
interpretación de los resultados. De acuerdo a la problemática y a los
objetivos propuestos el proyecto se ubica en el campo del paradigma interpretativo
o cualitativo, con un enfoque crítico social que asume el método de
investigación acción (IA). Empezando por los aportes de (Borda, 1987) quien
considera la IA como una acción como una actividad transformadora, militante y
comprometida. Así mismo, se definen las actividades diseñadas y aplicadas en
las diferentes fases de la investigación; al igual que los instrumentos para la
recolección de información. Finalmente, se presentan los resultados y hallazgos
del proyecto.
Descripción
del problema
El proyecto se ejecutó en La IE La Magdalena,
sede Marco Fidel Suárez enfocado principalmente en estudiantes de básica
primaria (4º y 5º), que se encuentran en un rango de edades que van de 9 a12
años, totalizando la muestra a 22 estudiantes. Esta población estudiantil
pertenece a familias estratificadas en los niveles 1 y 2 según la
caracterización del SISBEN. Las fuentes de ingresos de estas familias de
derivan de actividades agrícolas y pecuarias, la construcción y el servicio
doméstico para el caso de las mujeres, en su mayoría los adultos de estos
núcleos familiares no cuentan con niveles básicos de formación académica.
La problemática abordada en este proyecto de
intervención surge desde la lectura y el seguimiento al comportamiento de los
desempeños de los estudiantes en las pruebas saber de Matemáticas aplicadas en
grados 3° y 5° de la IE La Magdalena en la sede Marco Fidel Suárez entre los
años 2009 y 2015, estos resultados reflejan un indicador alto de estudiantes
que no alcanzaron los desempeños mínimos dentro del componente formulación y
resolución de problemas. Al respecto el Ministerio de Educación Nacional expone
que:
La formulación, el
tratamiento y la resolución de los problemas suscitados por una situación
problema permiten desarrollar una actitud mental perseverante e inquisitiva,
desplegar una serie de estrategias para resolverlos, encontrar resultados,
verificar e interpretar lo razonable de ellos, modificar condiciones y originar
otros problemas. (MEN, 2006)
Algunos de los hallazgos derivados del
análisis de estas pruebas permitieron determinar dificultades a nivel de
comprensión conceptual y operacional relacionadas con:
·
Formular
y resolver problemas que involucran estructuras aditivas de comparación,
igualación y combinación.
·
Formular
y resolver problemas que involucran estructuras multiplicativas simples.
·
Resolver
problemas con dos operaciones que requieren el uso de la adición para la
composición o la transformación.
La tradición en los trabajos de investigación
en matemáticas ha hecho énfasis en la compresión del dominio matemático y su
estrecha y siempre presente relación con las diferentes actividades que
realizan los sujetos en diferentes contextos, por lo cual la competencia
matemática como:
La capacidad
individual para identificar y comprender el papel que desempeñan las
matemáticas en el mundo, emitir juicios bien fundados, utilizar las matemáticas
y comprometerse con ellas, y satisfacer las necesidades de la vida personal
como ciudadano constructivo, comprometido y reflexivo (Rico, 2006)
Se puede deducir que las matemáticas
desempeñan un papel esencial en nuestras actividades diarias. En este sentido,
es crucial reconsiderar las matemáticas como un proceso de reflexión constante
que ayude a los estudiantes a entender la simbología abstracta del campo
matemático y su relevancia en situaciones cotidianas.
Un desafío importante es la falta de interés
de los estudiantes hacia las matemáticas y la percepción negativa que algunos
tienen de los maestros de la materia. Por lo tanto, es imperativo desarrollar y
aplicar estrategias didácticas atractivas que fomenten el interés de los
estudiantes en el conocimiento matemático. Los maestros deben tener un amplio
dominio del contenido matemático para guiar de manera efectiva a sus alumnos, lo
que contribuirá a mejorar la calidad de la educación matemática.
La escuela tiene la responsabilidad
primordial de crear entornos de aprendizaje óptimos que promuevan la
comprensión del conocimiento matemático. Por lo tanto, cada actividad educativa
debe dirigirse hacia la formalización de estructuras mentales que permitan a
los estudiantes comprender el verdadero propósito y aplicación de las
matemáticas.
Dadas estas circunstancias, se vuelve
esencial que desde el ámbito escolar y mediante prácticas pedagógicas
adecuadas, se creen y se sugieran enfoques metodológicos que promuevan la
consolidación del entendimiento matemático como una herramienta fundamental
para enfrentar los desafíos de la vida diaria, donde el uso de las matemáticas
adquiere relevancia. Por consiguiente, el trabajo de intervención actual se
enfoca en explorar la pregunta: ¿Cómo mejorar el dominio de estructuras aditivas
y multiplicativas en la solución de situaciones problema en los estudiantes de
básica primaria (4° y 5°) de la IE La Magdalena sede Marco Fidel Suárez? Esta
propuesta de intervención a partir de la problemática descrita se propuso se
orientó hacia el alcance de los siguientes objetivos: (1) Afianzar el
pensamiento numérico a través de solución de situaciones problema con base en
estructuras aditivas y multiplicativas; (2) Diseñar y aplicar pruebas
diagnósticas; (3) Ajustar el plan de aula enfocado a la solución de situaciones
problemas basadas en estructuras aditivas y multiplicativas; y (4) Realizar
seguimiento periódico al desempeño de los estudiantes en el área.
Referentes
de la investigación
El
razonamiento, una mirada a través de la historia de las matemáticas
La historia de la humanidad ha estado ligada
desde sus orígenes a la actividad matemática. Inicialmente, las matemáticas no
contaban con la formalidad de la misma ciencia, pero los relatos históricos dan
cuenta de la forma como el hombre primitivo se valía de diferentes métodos para
realizar cálculos y estimaciones simples. Un ejemplo de estos estos primeros
pasos hacia la formalización de lo abstracto del pensamiento matemático fue la
forma como el hombre primitivo construyó esquemas mentales para establecer
relaciones entre cantidades, incorporando la noción de conteo uno a uno
haciendo uso de elementos naturales del entorno. Marcando el inicio de lo que
más adelante conoceríamos como patrones y secuencias numéricas; proceso que se
describe en “Las Matemáticas a Lo Largo de la Historia: de la Prehistoria a la
Antigua Grecia”:
El método más comprobado universalmente en la
historia de la “contabilidad”, y también uno de los más antiguos, es el del
hueso pedazo de madera tallado. Método con el que el hombre pudo arreglarse en
una época en que todavía no sabía contar de manera abstracta. (Gutiérrez,
2009:11)
Las representaciones gráficas halladas en los
huesos de Ishango y de Brassempouy en los que se notaban de manera definida
marcas
grabadas en el peroné de un
babuino, hallazgo sobre el cuál se especula que este sistema de muescas
sucesivas representó un conteo para hacerse una idea de el paso del tiempo a
partir del registro de lunas y soles; razón por la que se le reconoce como el
vestigio más antiguo de la actividad matemática.
Las diferentes civilizaciones del mundo desde
el empirismo empezaron a consolidar actividades, pensamientos y procesos que
más adelante formalizarían las matemáticas como ciencia, pero fue solo hasta la
mitad del siglo VI a.c que alcanzaría la validez y el formalismo para ser
reconocida como ciencia a través de pensadores como Pitágoras, Aristóteles y
Euclides quienes fundaron las primeras escuelas del pensamiento en Grecia. En
opinión de Kant “La cultura griega encontraría, el camino real para la
matemática por la obra de Tales, Pitágoras y las diversas generaciones de
Pitagóricos de los siglos posteriores”. (Loyes, 1993:27)
Competencia
matemática
Para el caso Colombia, se inicia la
apropiación de un modelo educativo basado en competencias, presentado como el
horizonte encaminado hacia la formación integral de los estudiantes que
permitiría el desarrollo de capacidades para desenvolverse en diferentes
situaciones de la cotidianidad de manera efectiva. Dentro de este modelo se
incorpora el concepto de competencia a partir de lo propuesto por Pérez, A.,
Lobato, C., García, E., De Miguel, M., Arias, J., Apodaca, J., Alfaro, I.
(2006), quienes la definen como
…Un proceso de
aprendizaje y enseñanza que se desarrolla a lo largo de toda la vida y que
contribuye a la formación integral de las personas, al pleno desarrollo de sus
potencialidades, a la creación de cultura. La cual se desarrolla en
instituciones educativas y en diferentes ámbitos de la sociedad. (Wilson
et al, 2006)
Del mismo modo, la competencia matemática en
el marco del proyecto PISA se define partiendo de la siguiente afirmación
El concepto de
competencia se identifica con el de proceso y pone el acento en lo que el
alumno es capaz de hacer con sus conocimientos y destrezas matemáticas, más que
en el dominio formal de dichos conceptos y destrezas. (Rico,
2006:58)
Resulta primordial considerar que cada uno de
los procesos implícitos en las competencias se centran
en el aprendizaje del estudiante el cual debe desarrollarlas para alcanzar un
nivel de comprensión que se fundamentan en el saber hacer a través competencias
específicas del pensamiento matemático. Estas competencias son “pensar y
razonar; Argumentar; Comunicar; Modelar; Plantear y resolver problemas;
Representar y Utilizar el lenguaje simbólico, formal y técnico y las
operaciones”. (Leyva y Proenza.2006:12)
Hacer referencia al dominio de la competencia
matemática requiere destacar la manera en que los estudiantes adquieren y
utilizan diversas estructuras de pensamiento que les permiten analizar, razonar
y comunicar ideas de manera efectiva, que los lleven a plantear, formular y
resolver situaciones diversas que enfrentan en su entorno. Este dominio de la
competencia matemática es sustentado desde perspectivas como la siguiente:
Una habilidad crucial
implícita en esta noción de la competencia matemática es la capacidad de plantear,
formular, resolver, e interpretar problemas empleando las matemáticas dentro de
una variedad de situaciones y contextos. Estos contextos van desde los
puramente matemáticos a aquellos que no presentan ninguna estructura matemática
aparente (en este caso la persona debe introducir ella misma la estructura
matemática). (Leyva y Proenza.2006:11)
Alcanzar el dominio de la competencia
matemática implica realizar una reflexión integral que involucre los datos
relevantes de diversas situaciones, los enunciados asociados y la estrategia de
solución que cada persona elige. Esto permite interpretar los problemas y
ofrecer respuestas adecuadas, adaptándose al nivel de dificultad que varía
según el contexto.
El niño
y la formalización del pensamiento matemático
Resulta conveniente reconocer que las
nociones matemáticas aprendidas por lo niños en su formación inicial
escolarizada y no escolarizada representan un andamiaje conceptual y operativo
importante para el desarrollo de las competencias matemáticas en grados
superiores. La configuración del pensamiento matemático involucra la compresión
de símbolos y lenguajes para la construcción de conceptos propios de las
matemáticas. La interiorización del aprendizaje del objeto matemático ha
mostrado mayor efectividad cuando el niño se relaciona con el mismo desde
temprana edad; ya que le permite un acercamiento con nociones, operaciones,
representaciones y modelaciones que lo preparan para elaborar esquemas mentales
más complejos que le permiten la comprensión del mundo a través del saber
matemático. En este sentido “se dice con frecuencia que, si se pusiera a los
niños en contacto con las ideas matemáticas, con su lenguaje y con sus símbolos
más temprano de lo que se acostumbra, los conceptos matemáticos se alcanzarían
antes” (Lovell, 1962:34).
Es a través del razonamiento matemático el
niño puede asumir un rol central en el ejercicio que le permita por medio de la
comprensión elaborar argumentos, planear y plantear soluciones, validarlas y
establecer conclusiones para dar alternativas de respuesta a la situación
propuesta. Esta postura invalida la noción de que las matemáticas solo se
pueden formalizar desde la memorización de algoritmos y postulados reconociendo
la importancia de las mismas en el desarrollo del pensamiento humano.
En el desarrollo del pensamiento matemático
en indispensable comprender las distintas etapas de desarrollo de los niños. En
este sentido, numerosos estudios señalan que no se trata simplemente de
impartir información de manera indiscriminada, sino más bien de construir
conocimiento a partir de las experiencias que se integran en la rutina diaria
de la escuela. Esta posición se argumenta desde la siguiente postura:
Los niños de nuestro
entorno, muestra lo que estos son capaces de hacer con la serie numérica antes
de llegar a la escuela. Han recibido gran información, en un principio de forma
memorística de la serie numérica y la mayoría de los niños de cuatro y medio a
seis años pueden llegar a contar hasta 29 o 39. (Castro, 2004:11:12)
En atención a las posturas anteriormente
expuestas el ejercicio matemático debe proponerse acercar al estudiante al
conocimiento desde lo vivencial, fomentando la capacidad de reflexionar desde
lo crítico la apropiación del pensamiento matemático a través de presaberes
hasta llegar a la formalización del mismo.
Creencias
y el desarrollo de la competencia matemática
La actividad matemática ha sido considerada a
lo largo de la historia como una de las disciplinas más complejas, esto debido
a la rigurosidad con la que se ha formulado desde sus inicios en la antigua
civilización griega. Que inicialmente propuso una serie de axiomas y pruebas
condujeron a conclusiones que iban más allá de simples operaciones aritméticas,
marcando así el inicio del pensamiento matemático orientado hacia el
razonamiento.
La naturaleza analítica y compleja de las
matemáticas han generado un conjunto de percepciones erróneas e ideas
informales que han limitado su misma comprensión y por consiguiente el progreso
de la competencia matemática. Aunque es cierto que las matemáticas son
cruciales para el desarrollo cognitivo, no resultan atractivas para todos, ya
que existen concepciones negativas arraigadas en torno a ellas. Estas
concepciones buscan justificar el bajo rendimiento de los estudiantes en
actividades que involucran las matemáticas.
Una aproximación al concepto de creencias es
aquella que las sugiere como “una forma de conocimiento personal y subjetivo,
que está más profunda y fuertemente arraigada que una opinión; se construyen a
través de las experiencias, informaciones y percepciones, etc., y de ellas se
desprenden unas prácticas”. (Vila y Callejo, 2004:46)
De tal modo puede afirmarse que las creencias
se configuran desde experiencias personales y que han se han establecido como
un tipo de conocimiento no formal, a través de opiniones que condicionan
posturas y actitudes frente han sido fuertemente arraigadas creando diferentes
posturas y actitudes frente a la realidad.
En la educación las creencias se han
originado desde diferentes factores y son asumidas como verdades personales que
se han ido arraigando mediante rutinas y repeticiones en contextos escolares y
culturales. Alrededor de las matemáticas se han creado una serie de creencias
que desfavorecen la enseñanza y el aprendizaje de estas; como por ejemplo que
la creencia de que las matemáticas solo pueden ser estudiadas por personas muy
inteligentes o en su defecto que las matemáticas son para “locos”.
Los contextos familiares y culturales también
han influido para argumentar una defensa al momento de tratar de comprender la
poca afinidad que tienen los estudiantes con la actividad matemática; ideas que
se formalizan a partir de supuestos que son elaborados desde experiencias
negativas que se expresan a partir de expresiones como “mi papá era pésimo para
las matemáticas”, “las matemáticas son el coco de todos los niños” o “yo para
qué aprendo matemáticas si no las voy a enseñar”. Estas creencias han generado
imaginarios colectivos que influyen negativamente en la enseñanza y el
aprendizaje de las matemáticas. El siguiente esquema refleja la relación entre
las creencias y la conducta que asume el estudiante a nivel cognitivo y
motivacional a la hora de estudiar matemáticas.
Figura
1.
Elementos que perjudican la conducta matemática del estudiante
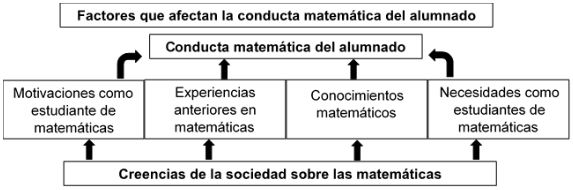
Fuente: Libro
Matemáticas para aprender a pensar “el papel de las creencias en la resolución
de problemas”. Antoni Vila Corts y Ma. Luz Callejo de la Vega, 2004:56
La
solución de problemas, una alternativa didáctica para la enseñanza de las
matemáticas
El enfoque de aprendizaje basado en problemas
se presenta como una alternativa que facilita la adquisición y consolidación de
conceptos matemáticos. Este método fomenta la reflexión, la modelación, la
comunicación y el ajuste de estructuras, culminando en la búsqueda de
soluciones que aborden la situación planteada. Una primera aproximación a la
definición de una situación problema plantea que: Una situación problema la
podemos interpretar como un contexto de participación colectiva para el
aprendizaje, en el que los estudiantes, al interactuar entre ellos mismos, y
con el profesor, a través del objeto de conocimiento, dinamizan su actividad
matemática, generando procesos conducentes a la construcción de nuevos
conocimientos. (Obando y Munera, 2003:185)
Frente a esto el Ministerio de Educación
Nacional ha emitido su postura y plantea la solución de situaciones problemas
como una estrategia que promueve el desarrollo de competencias matemáticas que
se demuestran mediante procesos como
Formular, plantear,
transformar y resolver problemas a partir de situaciones de la vida cotidiana,
de las otras ciencias y de las matemáticas mismas. Ello requiere analizar la
situación; identificar lo relevante en ella; establecer relaciones entre sus
componentes y con situaciones semejantes; formarse modelos mentales de ella y
representarlos externamente en distintos registros; formular distintos
problemas, posibles preguntas y posibles respuestas que surjan a partir de
ella. (MEN, 2006)
Se debe entender que toda actividad
matemática basada en la solución de situaciones problema se orienta para
generar la interiorización de aprendizajes y conocimientos que faciliten la
reflexión a medida que el estudiante avanza en estrategias de solución a partir
de sus propias heurísticas al momento de asumir la actividad matemática. Al
respecto Santos (2007) propone la solución de problemas como una forma de
pensar, en la cual el estudiante hace uso de diferentes estrategias y recursos
cognitivos que lo aproximan a la formalización y validación del aprendizaje de
las Matemáticas. Del mismo modo, Santos (2007) indica que: “El término problema
se vincula no solamente a situaciones específicas rutinarias o no rutinarias,
donde el estudiante intenta encontrar la solución, sino también incluye tener
que aprender algún concepto matemático”. Este planteamiento encuentra
consonancia con lo propuesto por Calvo y Salas (2009), puesto que consideran
que para desarrollar varias tareas se debe tener dominio del concepto
matemático.
Desde una perspectiva más amplia, se puede
entender que las situaciones problemáticas ofrecen un contexto para integrar
los conocimientos previamente adquiridos a través de la construcción de
conceptos que se han desarrollado a lo largo del recorrido educativo de un
estudiante. Esto requiere un proceso de reflexión y análisis que permita formar
una representación mental para determinar la estrategia hacia la solución del
problema específico que el estudiante enfrenta. En esta línea de pensamiento,
Mathiaud propone:
…Lo que,
en mi opinión,
da lugar a una verdadera
actividad matemática por parte del alumno, es la búsqueda de un problema que
utiliza y coordina los conceptos aprendidos por separado, o también un problema
que se inscriba dentro del proceso de aprendizaje de “un objeto” matemático.
(Mathiaud, 1996)
Actualmente el Ministerio de Educación
Nacional a través de los derechos básicos de aprendizaje (DBA), sugiere que la
solución de situaciones problema debe ser interiorizada en el quehacer de la enseñanza
de las matemáticas desde los niveles de educación inicial y que su complejidad
debe ser progresiva acorde con los niveles de escolaridad de los estudiantes.
También invita a realizar ejercicios de reflexión para cuestionar la forma cómo
se ha venido enseñando tradicionalmente las matemáticas y al mismo tiempo sobre
el papel fundamental de estrategias metodológicas para la educación de las
matemáticas; presentando como modelos de referencia el método Singapur y
recientemente el método Prest.
Estructuras
aditivas
Las estructuras aditivas se tipifican en
distintos modelos que facilitan la relación entre el objeto matemático y la
representación de la adición y la sustracción. Operaciones que por su nivel de
comprensión son enseñadas en los primeros años de escolarización atendiendo a
los niveles de desarrollo cognitivo acordes con la edad de los estudiantes.
Las estructuras aditivas presentan modelos de
representación y comprensión de situaciones contextualizadas a través de
enunciados que proporcionan a los estudiantes variables para que a partir de
ellas planteen esquemas conceptuales y alternativas de solución a la situación
problema que se propone.
Castro, Rico y Castro (1995) presentan
categorías de operaciones que pertenecen a la estructura aditiva. Estos modelos
son expuestos en el texto Estructuras Aritméticas Elementales y Su Modelización
de la siguiente manera:
Modelos
Lineales:
Estrategia que propone sucesiones numéricas para el conteo y comparación de
cantidades.
Modelos
Cardinales:
Usados en teoría de conjuntos e incluyen esquemas estáticos (no hay acción) o
dinámicos (la operación es el resultado de una acción).
Modelos
con medidas:
Usados como patrones de medida en la modelación y comparación de unidades.
Modelos
funcionales: Modelo
que representa el estado inicial de una cantidad que al ser alterado por un
operador refleja un cambio y un estado final. Modelo que se explica en el
siguiente esquema:
Figura
2.
Esquema funcional de la Adición
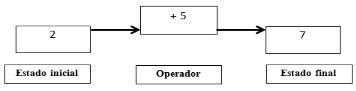
Fuente: Libro Estructuras Aritméticas
Elementales y Su Modelización. Encarnación Castro, Luis Rico y Enrique Castro,
1995:32.
Figura
3.
Esquema funcional de la sustracción
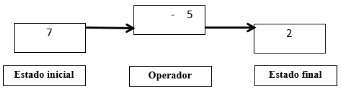
Fuente: Libro
Estructuras Aritméticas Elementales y Su Modelización. Encarnación Castro, Luis
Rico y Enrique Castro, 1995:32.
En el campo de las estructuras aditivas se
establecen cuatro categorías que se relacionan a continuación:
Figura
4.
Esquema de categorías - estructura aditiva
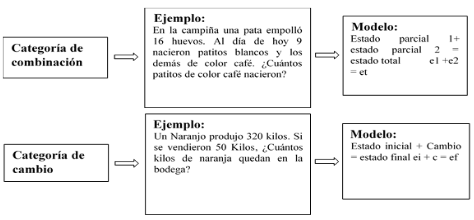
Estructura
multiplicativa
Las estructuras multiplicativas están
conformadas por el producto y el cociente, que son operaciones matemáticas que
representan un mayor nivel de complejidad y que su enseñanza requiere de un
conjunto de saberes previos (formalizados desde la comprensión de las
estructuras aditivas) teniendo en cuenta el nivel de desarrollo cognitivo de
los estudiantes.
El producto resulta de la suma de
repeticiones de sumandos “n” veces y el cociente se define como repartos
iguales de una cantidad que se relaciona con sustracciones sucesivas de
cantidades iguales.
Para esta estructura Castro, Rico y Castro
(1995) presentan seis modelos para comprender las operaciones producto y
cociente. Estos modelos son:
Modelos
Lineales: El
producto representa la suma de una sucesión numérica que se repite “n” veces (n
x a) y el cociente representa un conteo regresivo de una constante determinada
por el divisor.
Modelos
Cardinales: Para
el producto se utilizan contextos cardinales como unión de conjuntos, producto
cartesiano entre otros, para entender el producto como una operación aritmética
básica. El cociente usa un esquema basado en repartir en partes iguales.
Modelos
con Medida:
Establece patrones de medidas con ayuda de las regletas de Cuisenaire y la
balanza como herramienta para comprender el objeto matemático a partir de
comparaciones y equivalencias de unidades.
Modelos Numéricos: Uso de números para
representar simbólicamente operaciones, para el caso del producto un modelo es:
6 x 3 = Sumar 6 veces 3, por lo tanto, se puede representar como una adición de
sumandos repetidos así: 3 + 3 + 3 + 3 + 3 + 3
Para el caso del cociente, representado por
sustracciones sucesivas determinando la cantidad a restar desde el cociente
hasta llegar a una cantidad irreducible, tal como es el siguiente caso: 18: 6
entonces se determina así: 18 – 6 = 12  12 – 6 = 6,
12 – 6 = 6,
y finalmente 6 – 6 =
0.
Modelos
de Razón Aritmética:
Involucra la comparación entre conjuntos en relación a “cuántas veces más”
hasta hallar el factor de transformación o comparación.
Modelos
funcionales:
Estructura operatoria que convierte los números por la influencia de un
operador, modelo que se representa a continuación:
Figura
5.
Esquema funcional del producto
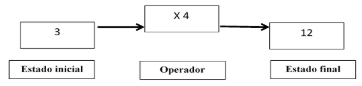
Fuente: Libro
Estructuras Aritméticas Elementales y Su Modelización. Encarnación Castro, Luis
Rico y Enrique Castro, 1995:55.
Figura
6.
Esquema funcional del cociente
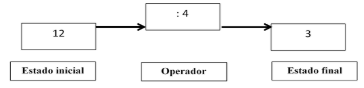
Fuente: Libro
Estructuras Aritméticas Elementales y Su Modelización. Encarnación Castro, Luis
Rico y Enrique Castro, 1995:55.
En el campo de las estructuras
multiplicativas se distinguen dos categorías, la primera es el isomorfismo de
medida y la segunda el producto de medida, categorías que definen las
operaciones implícitas dentro de estas estructuras tal como se exponen a
continuación:
Figura
7.
Esquema de categorías - estructuras Multiplicativas
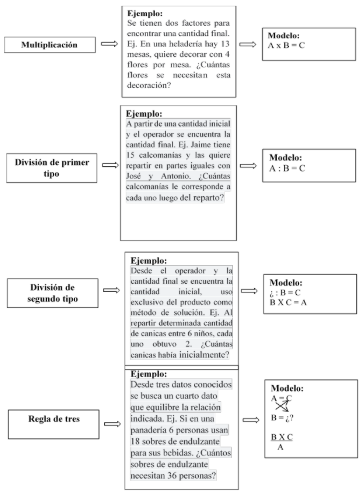
Fuente: Los autores
Figura
8.
Esquema de categorías - estructuras Multiplicativas

Fuente: Los autores
MÉTODO
Investigación,
enfoque y método
La investigación de la que se deriva la
estrategia “La granja matemática” herramienta didáctica para solución de
situaciones problema” se enmarca dentro de los encuadres teóricos y
metodológicos de La Investigación Acción (IA). Esta metodología se caracteriza
principalmente por ser un modelo transformador (Borda, 1987) y surge como un
modelo alternativo al paradigma clásico que presentaba ciertas limitaciones
para comprender e interpretar problemáticas sociales. La Investigación Acción
se define conceptual y metodológicamente como un término genérico que incluye
diferentes estrategias de intervención que se llevan a cabo con el fin de
transformar y mejorar realidades en contextos sociales y educativos (Latorre,
2003).
En el marco de la investigación cualitativa,
este estudio se enfocó en el método de Investigación Acción, que implica
abordar de manera deliberada la resolución de una problemática identificada.
Dada la naturaleza y los objetivos del estudio, la perspectiva metodológica
adoptada se enmarca en los principios teóricos y conceptuales de la
investigación cualitativa, que se caracteriza por un interés en comprender cómo
los participantes en el estudio perciben y dan significado a los temas
investigados (Fraenkel y Wallen, 1996). De esta manera, el investigador buscará
reconstruir la realidad según la experiencia y las perspectivas de los
participantes, utilizando datos que proporcionen una visión más completa de sus
puntos de vista.
Diseño
metodológico
La ruta metodológica para el desarrollo de
esta estrategia fue diseñada ejecutando los siguientes pasos:
1.
Rastreo
teórico del objeto de estudio.
2.
Aplicación
de prueba diagnóstica como referencia para el inicio del caso.
3.
Transformación
de la problemática y el comportamiento de la población de estudio durante la
recolección de datos.
4.
Determinar
el impacto de la intervención.
5.
Triangulación
de la problemática con los referentes teóricos
6.
Conclusiones
e implicaciones derivadas de la investigación.
Se diseñaron y
aplicaron tres secuencias didácticas distribuidas en 10 sesiones de
intervención en el aula, donde se abordó pedagógica y didácticamente una
categoría de las estructuras en estudio por sesión, las cuales fueron
trabajadas con una duración de dos horas por semana, teniendo una duración
total 10 semanas y 20 sesiones.
El diseño de cada sesión se organizó de la
siguiente manera: En la sesión número uno se trabajó la relación comunicativa
entre concepto, proceso y acción; aplicación en situaciones cotidianas. En la
sesión dos se realizó una prueba que buscaba medir
proceso de comprensión y apropiación de los conceptos trabajados previamente y
así establecer la eficacia de la propuesta.
RESULTADOS
Diagnóstico
Planificación: Como método de investigación
para recopilar datos en el marco de este proyecto de intervención, se empleó el
estudio de casos, una metodología que ha ganado popularidad en diversas áreas,
incluyendo las matemáticas. Trabajar con este enfoque proporcionó una variedad
de recursos para abordar y relacionar la población estudiada con el fenómeno de
interés.
Por lo tanto el
método de estudio de caso es una herramienta valiosa de investigación, y su
mayor fortaleza radica en que a través del mismo se mide y registra la conducta
de las personas involucradas en el fenómeno estudiado, mientras que los métodos
cuantitativos sólo se centran en información verbal obtenida a través de encuestas
por cuestionarios (Yin, 1989). desde una variedad de fuentes
cualitativas o cuantitativas a partir de fuentes escritas, registros de
archivos, entrevistas directas, observación directa, observación de los
participantes e instalaciones u objetos físicos (Chetty, 1996) citado en
(Martínez, 2006:167)
El enfoque socioeducativo del estudio de
casos ofrece diversas ventajas para la investigación tales como: la
profundización, la pertinencia para investigaciones de magnitudes pequeñas,
permite la toma de decisiones, así como la participación de otros agentes, es
útil para la investigación desde el quehacer del docente, involucra trabajo
cooperativo y la interdisciplinariedad. Dentro de esta primera etapa se propuso
como objetivo principal caracterizar y analizar el estado inicial del
estudiantado en relación a la problemática abordada a través de la aplicación
de una prueba diagnóstica (taller vivencial). Esto permitió tener un
acercamiento a las percepciones de los estudiantes frente a la actividad
matemática desde la solución de situaciones problema de naturaleza aditiva y
multiplicativa. Este taller vivencial permitió la recolección de elementos
significativos como punto de partida para la propuesta de intervención ya que:
Ésta es una
estrategia de particular importancia en los proyectos de investigación acción
participativa. Su fortaleza principal estriba en la posibilidad que brinda el
abordar, desde una perspectiva integral y participativa, situaciones sociales
que requieren algún cambio o desarrollo. Esto incluye partir desde el
diagnóstico de tales situaciones, hasta la definición y formulación de un plan
específico de cambio o desarrollo, pasando por sus etapas intermedias, por la
identificación y valoración de las alternativas
más viables de
acción. (Casilimas, 2002:146:147)
Acción
Esta fase fue integrada por un conjunto de
actividades que consolidaron la estrategia de intervención y delimitaron el
camino hacia el logro de los objetivos. Para el diseño de la estrategia se
tuvieron en cuenta los referentes nacionales de calidad para el área de
matemáticas establecidos por Ministerio de Educación Nacional (MEN) en los
lineamientos curriculares, los estándares básicos de competencia y los derechos
básicos de aprendizaje (DBA), a partir de los cuales se pudo determinar la
siguiente relación:
Tabla
1.
Las estructuras aditivas y multiplicativas a la luz de los estándares
|
ESTÁNDARES
|
ÁREA
|
ACTIVIDAD
|
|
Resuelvo y formulo problemas en situaciones aditivas de composición,
transformación, comparación e igualación
|
MATEMÁTICAS
|
Jugando y razonando.
|
|
Uso diversas estratégicas de cálculo y estimación para resolver
problemas en situaciones aditivas y multiplicativas.
|
MATEMÁTICAS
|
Un problema para cada situación, una solución para cada problema.
|
|
Interpreta, formula y resuelve problemas aditivos de composición,
transformación y comparación en diferentes contextos; y multiplicativos,
directos e inversos, en diferentes contextos.
|
MATEMÁTICAS
|
Las matemáticas son divertidas.
|
El desarrollo de estas actividades tuvo como
propósito establecer un marco de referencia para el proyecto a partir de las
disposiciones nacionales para el área de matemáticas con el fin de verificar la
validez de la propuesta. Igualmente se pudo demostrar la pertinencia del uso de
situaciones problemas con uso de las estructuras aditivas y multiplicativas en
correspondencia con lo que demanda ser competentes en matemáticas.
Comentario: En el proceso de investigación la
observación representa un recurso importante al momento de recolectar datos
para la validación conceptual de las categorías y para la continua reflexión de
los resultados que permiten elaborar conclusiones al mismo tiempo que
determinara la eficacia del proceso de investigación. Durante esta fase del
proyecto, se empleó la observación participante como método para recopilar
datos. Este enfoque reveló situaciones notables que surgieron de manera
orgánica en el grupo estudiado, destacando tanto los progresos realizados como
el impacto percibido de la propuesta. En este punto, fue crucial aplicar un alto
nivel de perspicacia para interpretar las percepciones de los estudiantes y sus
conocimientos previos.
Reflexión: Esta etapa de reflexión representa
un pilar fundamental en el campo de la investigación acción puesto que permite
replantear y rediseñar de manera paralela a la ejecución del proyecto a través
de la toma de decisiones con el objetivo de lograr una efectiva transformación
de la problemática. Después de llevar a cabo las actividades planificadas, se
empleó este proceso de reflexión para analizar los resultados observados
durante la ejecución de la propuesta. El objetivo era proporcionar
retroalimentación a los docentes y estudiantes sobre los procesos en los que
estuvieron involucrados.
Secuencias
didácticas en la implementación de la estrategia
Durante la implementación de las secuencias
didácticas se utilizó el diario de campo como instrumento de registro y
seguimiento a los aportes de cada niño durante las actividades propuestas desde
la intervención, las actividades estuvieron apoyadas con el uso de recursos
didácticos y tecnológicos. Así mismo, se hicieron jornadas de trabajo en
espacios al aire libre como la huerta escolar. Estas secuencias didácticas
favorecieron y afianzaron el trabajo cooperativo y la integración de los
estudiantes, pudo observarse también alta motivación frente al desarrollo de
las actividades planteadas y el uso de los diferentes recursos.
Al abordar situaciones contextualizadas que
eran familiares para los estudiantes, fue posible interpretar mejor los
escenarios planteados. Esto facilitó un progreso más rápido en la comprensión
de las características de las estructuras presentadas, lo que permitió a los
estudiantes interiorizar y diseñar de manera más sencilla la ruta necesaria
para llegar a una conclusión que abordara el problema planteado.
Tabla
2.
Secuencia didáctica 1
|
Título de la secuencia: Jugando y Razonando
|
|
Título de la secuencia didáctica:
Jugando y Razonando.
Institución Educativa:
La Magdalena
Dirección: Corregimiento La Habana.
Docentes Responsables:
Julián Montoya – Yenny Giraldo Área de conocimiento: Matemáticas.
Grados: Cuarto y Quinto.
|
Secuencia didáctica # 1 Sede educativa:
Marco Fidel Suárez
Municipio: Guadalajara de Buga. Departamento: Valle del Cauca. Tema:
Estructuras aditivas.
Tiempo: 4 semanas.
|
|
Propósito de la secuencia
|
|
Al concluir la ejecución de la secuencia los estudiantes de 4° y 5° de
la IE La Magdalena sede Marco Fidel Suárez habrán apropiado los elementos
conceptuales necesarios para reconocer las estructuras aditivas y solucionar
situaciones problema.
|
|
Objetivos, competencias y contenidos
|
|
Objetivo de aprendizaje: Reconocer las estructuras aditivas y su
aplicación en la solución de situaciones problema del contexto.
Contenidos a desarrollar: Categoría de cambio, comparación, combinación
e igualación.
|
|
Estándares Básicos de Competencias
|
|
Resuelvo y formulo problemas en situaciones aditivas de composición
(combinación), transformación (cambio), comparación e igualación.
|
|
Derecho Básicos de Aprendizaje (DBA)
|
|
Interpreta, formula y resuelve problemas aditivos de composición,
transformación y comparación en diferentes contextos; y multiplicativos,
directos e inversos en diferentes contextos.
|
|
|
Metodología
|
|
Fase
|
Actividades
|
|
Sensibilización
|
Se plantea a los estudiantes una situación problema basada en la
estructura aditiva de estudio de acuerdo al orden establecido, para luego
orientar preguntas de enfoque, por ejemplo: ¿Qué me plantean en la situación
problema? ¿Tengo clara la operación implicada en la situación problema? ¿Hay
una única ruta para resolver la situación problema planteada? ¿Puedes inferir
una conclusión a partir de la situación problema planteada?
A partir de los conocimientos previos de los estudiantes se brinda el
soporte conceptual de cada una de las categorías de las estructuras aditivas.
|
|
Motivación
|
En esta fase los estudiantes desarrollarán una actividad de conjunto
donde tienen la tarea de resolver una situación problema basada en la
categoría de estudio para cada semana. Se orientará a los estudiantes para
que representen el problema con elementos concretos que permitan explicar de
manera clara y tangible los procesos elaborados para llegar a la solución del
problema planteado.
En esta fase los estudiantes desarrollarán una actividad de conjunto
donde tienen la tarea de resolver una situación problema basada en la
categoría de estudio para cada semana. Se orientará a los estudiantes para
que representen el problema con elementos concretos que permitan explicar de
manera clara y tangible los procesos elaborados para llegar a la solución del
problema planteado.
Por ejemplo: A Camilo le regalaron 7 conejos del proyecto escolar. A
Laura le regalaron 5 conejos más que a camilo. ¿Cuántos conejos le regalaron
a Laura?
¿Qué operación te ayudará a encontrar la
respuesta?
|
|
Aplicación
|
Para esta etapa de la sesión los estudiantes deberán resolver cada una
de las fichas de trabajo diseñadas para la apropiación del objeto de estudio,
en formato de taller escrito previamente estructurado que contiene ejercicios
que involucran el uso de estructuras aditivas (cambio, comparación,
combinación e igualación) en la solución de situaciones problema.
|
|
Producción
|
Para esta fase se espera que una vez apropiados los esquemas de cada
categoría los estudiantes estén en la capacidad de planear, formular y
resolver situaciones problema de sus contextos.
|
|
|
RECURSOS
|
|
Nombre del Recurso
Fichas de trabajo Videos
Hojas de block Lápiz
|
Descripción del recurso
Fichas de trabajo enfocadas temáticamente a cada categoría de estudio
(4 en total)
Material videográfico que permita visualizar alguna de las situaciones
planteadas.
Materiales usados diariamente para la actividad escolar
|
|
Evaluación y recursos asociados
|
|
Para evaluar las actividades se tendrán en cuenta los siguientes
criterios:
Actitud de los estudiantes frente a las actividades propuestas.
Modelación y representación de la situación problema.
Claridad en los procesos.
Argumentación de las respuestas.
Trabajo en equipo.
|
|
Instrumentos de Evaluación
|
|
Se diseñará un formato de instrumento de evaluación en el que se
especifican los criterios a tener en cuenta para la evaluación y verificación
de la participación de los estudiantes durante el proceso (se anexa
instrumento de evaluación).
Las fichas de trabajo desarrolladas por los estudiantes se conservarán
para hacer
retroalimentación del proceso en la institución
|
|
Bibliografía
|
|
Encarnación Castro, Luis Rico, Enrique Castro. (1995). Estructuras
aritméticas y su modelación. Bogotá: Grupo Editorial Iberoamérica.
Ministerio de Educación Nacional (MEN). (2017). Vamos a aprender matemáticas.
Bogotá: Ediciones SM. S.A.
|
Tabla
3.
Rúbrica de Evaluación
|
INSTRUMENTO DE EVALUACIÓN
|
|
Nombre del Estudiante:
|
|
|
|
CRITERIO
|
SI
|
NO
|
|
Participa activamente en las actividades propuestas por el docente.
|
|
|
Representa y modela acertadamente la situación problema planteada.
|
|
|
Evidencia claridad en los procesos realizados para la solución de la
situación problema planteada.
|
|
|
Argumenta y justifica de manera detallada las respuestas obtenidas.
|
|
|
Fomenta el trabajo cooperativo y grupal.
|
|
Análisis secuencia didáctica #1. Se
organizaron sesiones de trabajo en las que los estudiantes se organizaron en
grupos de trabajo con 5 integrantes, con el objetivo de comenzar actividades
de sensibilización. Inicialmente,
surgieron dificultades en las relaciones interpersonales, ya que
algunos estudiantes mostraban resistencia a trabajar con compañeros diferentes
a los grupos establecidos previamente. Sin embargo, al implementar estrategias
como juegos y rondas, se crearon nuevos lazos entre ellos.
Durante las dos primeras sesiones, los
estudiantes mostraron desinterés y falta de confianza al responder preguntas de
enfoque, evidenciando timidez y poca motivación para participar. Sin embargo,
en las siguientes sesiones, se observó un cambio de actitud, con mayor
participación y capacidad para comprender las estructuras estudiadas. Esto
mejoró significativamente la interacción entre docentes y estudiantes.
Al comenzar con la primera sesión sobre
categorías aditivas, se notó una falta de entusiasmo generalizada hacia las
actividades matemáticas. Los estudiantes preferían realizar actividades
diferentes, como cantar o bailar, que no implicaran tanto trabajo matemático
adicional al horario escolar establecido. Sin embargo, a medida que avanzaban
las sesiones del proyecto de intervención, se observó un cambio positivo en la
actitud de los estudiantes hacia las matemáticas, reconociendo su relevancia en
la vida cotidiana. Durante el desarrollo de las sesiones que abordaban
estructuras aditivas, los estudiantes enfrentaron dificultades para seleccionar
la operación matemática adecuada para resolver los problemas planteados. Sin
embargo, con el tiempo, mostraron mejoras a medida que se familiarizaban con
las estructuras, reduciendo la confusión y mejorando su desempeño.
Los padres de familia mostraron disposición
para involucrarse en el proyecto, lo que contribuyó positivamente al proceso de
aprendizaje de sus hijos. Participaron activamente resolviendo algunas
actividades diseñadas y cambiaron su percepción hacia las dificultades
matemáticas. Este compromiso familiar fue crucial para el éxito del proyecto,
ya que influyó positivamente en el rendimiento de los estudiantes en
matemáticas. En general, el proyecto logró cambiar la forma en que los padres
de familia veían las matemáticas, lo que ayudó a mejorar el rendimiento de los
estudiantes en esta área.
Tabla
4.
Secuencia didáctica 2
|
Título de la secuencia: Jugando y Razonando
|
|
Título de la secuencia didáctica:
Un problema para cada situación, una solución para cada problema.
Institución Educativa:
La Magdalena
Dirección: Corregimiento La Habana.
Docentes Responsables:
Julián Montoya – Yenny Giraldo Área de conocimiento: Matemáticas.
Grados: Cuarto y Quinto.
|
Secuencia didáctica # 2 Sede educativa:
Marco Fidel Suárez
Municipio: Guadalajara de Buga. Departamento: Valle del Cauca. Tema:
Estructuras Multiplicativas Tiempo: 4 semanas.
|
|
Propósito de la secuencia
|
|
Al concluir la ejecución de la secuencia los estudiantes de 4° y 5° de
la IE La Magdalena sede Marco Fidel Suárez habrán apropiado los elementos
conceptuales necesarios para reconocer las estructuras multiplicativas
comprendidas en la categoría de producto de isomorfismo y podrán analizar y
solucionar situaciones problemas.
|
|
Objetivos, competencias y contenidos
|
|
Objetivo de aprendizaje: Reconocer las estructuras multiplicativas y
su aplicación en la solución de situaciones problema del contexto.
Contenidos a desarrollar: Categoría de producto, de cociente de primer
y segundo tipo.
|
|
Estándares Básicos de Competencias
|
|
Uso diversa estrategias de cálculo y de estimación para resolver
problemas en situaciones aditivas y multiplicativas.
|
|
Derecho Básicos de Aprendizaje (DBA)
|
|
Interpreta, formula y resuelve problemas aditivos de composición, transformación
y comparación en diferentes contextos; y multiplicativos, directos e inversos
en diferentes contextos.
|
|
Metodología
|
|
Fase
|
|
Actividades
|
|
Sensibilización
|
Se plantea a los estudiantes una situación problema basada en la
estructura multiplicativa de estudio de acuerdo al orden establecido, para
luego orientar preguntas de enfoque, por ejemplo: ¿Qué me plantean en la
situación problema? ¿Tengo clara la operación implicada en la situación
problema? ¿Hay una única ruta para resolver la situación problema planteada?
¿Puedes inferir una conclusión a partir de la situación problema planteada?
A partir de los conocimientos previos de los estudiantes se brinda el
soporte conceptual de cada una de las categorías de las estructuras
multiplicativas.
|
|
Motivación
|
En esta fase los estudiantes desarrollarán una actividad de conjunto
donde tienen la tarea de resolver una situación problema basada en la
categoría de estudio para cada semana. Se orientará a los estudiantes para
que representen el problema con elementos concretos que permitan explicar de
manera clara y tangible los procesos elaborados para llegar a la solución del
problema planteado.
Por ejemplo: Un camión transporta 275 jaulas de pollo en pie. Si cada
jaula contiene 25 pollos. ¿Cuántos pollos transporta el camión? ¿Qué
operación te ayudará a encontrar la respuesta?
|
|
|
|
|
Fase
|
Actividades
|
|
Aplicación
|
Para esta etapa de la sesión los estudiantes deberán resolver cada una
de las fichas de trabajo diseñadas para la apropiación del objeto de estudio,
en formato de taller escrito previamente estructurado que contiene ejercicios
que involucran el uso de estructuras multiplicativas (producto, cociente de
primer y de segundo tipo) En la solución de situaciones problema.
|
|
Producción
|
esquemas de cada categoría los estudiantes estén en la capacidad de planear,
formular y resolver situaciones problema de sus contextos.
|
|
|
RECURSOS
|
|
Nombre del Recurso
Fichas de trabajo Videos
Hojas de block Lápiz
|
Descripción del recurso
Fichas de trabajo enfocadas temáticamente a cada categoría de estudio
(3 en total)
Material videográfico que permita visualizar alguna de las situaciones
planteadas.
Materiales usados diariamente para la actividad escolar.
|
|
|
Evaluación y recursos asociados
|
|
Para evaluar las actividades se tendrán en cuenta los siguientes
criterios:
Actitud de los estudiantes frente a las actividades propuestas.
Modelación y representación de la situación problema.
Claridad en los procesos.
Argumentación de las respuestas.
Trabajo en equipo
|
|
|
Instrumentos de Evaluación
|
|
Se diseñará un formato de instrumento de evaluación en el que se
especifican los criterios a tener en cuenta para la evaluación y verificación
de la participación de los estudiantes durante el proceso (se anexa
instrumento de evaluación).
Las fichas de trabajo desarrolladas por los estudiantes se conservarán
para hacer
retroalimentación del proceso en la institución
|
|
Bibliografía
|
|
Encarnación Castro, Luis Rico, Enrique Castro. (1995). Estructuras
aritméticas y su modelación. Bogotá: Grupo Editorial Iberoamérica.
Ministerio de Educación Nacional (MEN). (2017). Vamos a aprender matemáticas. Bogotá: Ediciones SM. S.A.
|
Análisis de la secuencia didáctica #2. La
implementación de la secuencia didáctica continuó empleando actividades
grupales como método de participación, lo que facilitó una visión holística de
las diversas formas en que los estudiantes comprenden las situaciones
matemáticas. El trabajo en grupo también fomentó solidaridad y colaboración en
la búsqueda de soluciones para problemas de interés común.
Durante la aplicación de la secuencia
didáctica, se identificaron vacíos conceptuales en los estudiantes,
especialmente en relación con los conceptos de producto y cociente, que se han
generado a lo largo de su escolarización. El manejo de algoritmos más complejos
resultó especialmente desafiante, con dificultades notables en la parte
procedimental de los algoritmos del producto y del cociente.
Pese a estos desafíos, la participación de
los estudiantes en las sesiones fue dinámica y con una buena asistencia. La
importancia de la propuesta para el desarrollo de las competencias matemáticas
se destacó, aunque hubo casos de estudiantes que mostraron resistencia
ocasional. A medida que avanzaba la ejecución se observaba cómo los estudiantes
hacían inferencias para resolver los problemas planteados, lo que respaldaba la
validez de la propuesta
Tabla
5.
Secuencia didáctica 3
|
Título de la secuencia: Jugando y Razonando
|
|
Título de la secuencia didáctica: Las matemáticas son divertidas.
Institución Educativa:
La Magdalena
Dirección: Corregimiento La Habana.
Docentes Responsables:
Julián Montoya – Yenny Giraldo Área de conocimiento: Matemáticas.
Grados: Cuarto y Quinto.
|
Secuencia didáctica # 3 Sede educativa:
Marco Fidel Suárez
Municipio: Guadalajara de Buga. Departamento: Valle del Cauca. Tema:
Estructuras Multiplicativas Tiempo: 2 semanas.
|
|
Propósito de la secuencia
|
|
Al concluir la ejecución de la secuencia los estudiantes de 4° y 5° de
la IE La Magdalena sede Marco Fidel Suárez habrán apropiado los elementos
conceptuales necesarios para reconocer tres de las estructuras
multiplicativas comprendidas en la categoría de producto de isomorfismo y
podrán analizar y solucionar situaciones problemas.
|
|
Objetivos, competencias y contenidos
|
|
Objetivo de aprendizaje: Reconocer las estructuras multiplicativas y
su aplicación en la solución de situaciones problema del contexto.
Contenidos a desarrollar: Categoría de regla de tres caso general y
categoría de producto (área, volumen y capacidad).
|
|
Estándares Básicos de Competencias
|
|
Resuelvo y formulo problemas en situaciones de proporcionalidad
directa, inversa y de producto de medidas.
|
|
Derecho Básicos de Aprendizaje (DBA)
|
|
Interpreta, formula y resuelve problemas aditivos de composición,
transformación y comparación en diferentes contextos; y multiplicativos,
directos e inversos en diferentes contextos.
|
|
|
Metodología
|
|
Fase
|
Actividades
|
|
Sensibilización
|
Se plantea a los estudiantes una situación problema basada en la
estructura multiplicativa de estudio de acuerdo al orden establecido, para
luego orientar preguntas de enfoque, por ejemplo: ¿Qué me plantean en la
situación problema? ¿Tengo clara la operación implicada en la situación
problema? ¿Hay una única ruta para resolver la situación problema planteada?
¿Puedes inferir una conclusión a partir de la situación problema planteada?
A partir de los conocimientos previos de los estudiantes se brinda el
soporte conceptual de cada una de las categorías de las estructuras
multiplicativas.
|
|
Motivación
|
En esta fase los estudiantes desarrollarán una actividad de conjunto
donde tienen la tarea de resolver una situación problema basada en la
categoría de estudio para cada semana. Se orientará a los estudiantes para
que representen el problema con elementos concretos que permitan explicar de
manera clara y tangible los procesos elaborados para llegar a la solución del
problema planteado.
Por ejemplo: En la panadería de La Habana, 5 clientes utilizan 12
cubos de azúcar para endulzar su café. Si 30 clientes necesitan endulzar el
café.
¿Cuántos cubos de azúcar serán necesarios? ¿Qué operación te ayudará a encontrar la respuesta?
|
|
Aplicación
|
Para esta etapa de la sesión los estudiantes deberán resolver cada una
de las fichas de trabajo diseñadas para la apropiación del objeto de estudio,
en formato de taller escrito previamente estructurado que contiene ejercicios
que involucran el uso de estructuras multiplicativas (producto de medida y
caso de, cociente de primer y de segundo tipo) En la solución de situaciones
problema.
En esta fase los estudiantes empiezan a trabaja la estrategia
didáctica diseñada por los autores para una mejor apropiación y ejercitación
del objeto de estudio.
La descripción de la estrategia y las reglas de juego se hacen en el
análisis de la siguiente secuencia.
|
|
Producción
|
Para esta fase se espera que una vez apropiados los esquemas de cada
categoría los estudiantes estén en la capacidad de planear, formular y
resolver situaciones problema de sus contextos.
|
|
|
RECURSOS
|
|
Nombre del Recurso
Fichas de trabajo Videos
Hojas de block Lápiz
Juego la granja
matemática
|
Descripción del recurso
Fichas de trabajo enfocadas temáticamente a cada categoría de estudio
(2 en total)
Estrategia didáctica diseñada por los autores de la propuesta, la cual
consiste en avanzar por un conjunto de juegos de mesa reforzando las
estructuras aditivas y multiplicativas en la solución de problemas.
Materiales usados diariamente para la actividad escolar.
|
|
Evaluación y recursos asociados
|
|
Para evaluar las actividades se tendrán en cuenta los siguientes
criterios:
Actitud de los estudiantes frente a las actividades propuestas.
Modelación y representación de la situación problema.
Claridad en los procesos.
Argumentación de las respuestas.
Trabajo en equipo.
|
|
Instrumentos de Evaluación
|
|
Se diseñará un formato de instrumento de evaluación en el que se
especifican los criterios a tener en cuenta para la evaluación y verificación
de la participación de los estudiantes durante el proceso (se anexa
instrumento de evaluación).
Las fichas de trabajo desarrolladas por los estudiantes se conservarán
para hacer
retroalimentación del proceso en la institución
|
|
Bibliografía
|
|
Encarnación Castro, Luis Rico, Enrique Castro. (1995). Estructuras
aritméticas y su modelación. Bogotá: Grupo Editorial Iberoamérica.
Ministerio de Educación Nacional (MEN). (2017). Vamos a aprender matemáticas. Bogotá: Ediciones SM. S.A.
|
Análisis Secuencia Didáctica #3. Durante la
implementación de esta etapa de trabajo en las secuencias didácticas, se
destacaron las actitudes positivas de los estudiantes hacia el trabajo en
equipo, reforzando la importancia del aprendizaje colaborativo para comprender
las estructuras matemáticas. Se identificaron líderes y se observaron
diferencias en los niveles de comprensión de las competencias matemáticas entre
los estudiantes, pero el trabajo en equipo permitió superar estas diferencias y
comprender mejor las estructuras en estudio.
La herramienta didáctica “La Granja
Matemática” se utilizó para reforzar el concepto de estructuras aditivas y
multiplicativas abordadas en el proyecto, promoviendo el trabajo en grupo, el
respeto y la reflexión. Este juego de mesa diseñado por los autores del
proyecto fue bien recibido por los estudiantes debido a su atractivo visual y
la oportunidad de aprender jugando, lo que llevó a que lo utilizaran incluso en
sus tiempos libres.
Las reglas del juego de “La Granja
Matemática” implican que los jugadores avancen por el tablero respondiendo
situaciones problemas relacionadas con las estructuras matemáticas, acumulando
puntos según sus respuestas. Esta herramienta resultó ser exitosa entre los
estudiantes, permitiéndoles comprender de manera vivencial las estructuras
matemáticas de manera práctica y didáctica.
El desarrollo de cada etapa del proyecto se
centró en propiciar prácticas escolares diferentes para fortalecer los procesos
matemáticos de los estudiantes, utilizando situaciones problema como
herramienta principal. Esta metodología facilitó el afianzamiento y la
apropiación de los conceptos matemáticos, aplicándolos en contextos concretos y
fomentando el razonamiento a partir de los datos planteados.
En este sentido Santos (2007) expone que “el
término problema se vincula no solamente a situaciones específicas rutinarias o
no rutinarias, donde el estudiante intenta encontrar la solución, sino también
incluye tener que aprender algún concepto matemático” y plantea la resolución
de problemas como una forma de pensar, donde el estudiante continuamente tiene
que desarrollar diversas habilidades y utilizar diferentes estrategias en su
aprendizaje de las Matemáticas. Estas ideas que van en la línea con lo
argumentado por Calvo y Salas (2008), puesto que consideran que el dominio de
ciertos conocimientos de forma combinada debe emplearse para desarrollar múltiples
tareas.
Figura
9.
La Granja Matemática

Fuente: fotografía de
los investigadores
A través de diálogos espontáneos establecidos
durante las sesiones de trabajo se observa que los estudiantes manifiestan
sentirse motivados por la forma como se orientó la actividad matemática a
través de la solución de situaciones problema. Los siguientes relatos dan
cuenta de esta afirmación: “Profe, cuando leí el problema encontré el nombre de
un lugar al que voy a bañar con mi familia”. (DC2.MFS.JM4). “Mira que en el
problema hablaba de un negocio que se parece al que tiene la mamá de Isabela
Jiménez” (DC5.MFS.JM16). “Trabajar matemáticas así es muy chévere porque se
pueden aprender jugando”. (DC8.MFS. JM25). “profe, cuando estaba resolviendo el
problema me di cuenta que podía responderlo haciendo operaciones diferentes y
el resultado no cambió” (DC7.MFS.JM14). “a mí me gusta trabajar las matemáticas
así porque puedo ver que las matemáticas son útiles en la casa, en la escuela,
en el trabajo, en cosas que uno hace todos los días, ¡JUMM
¡hasta pa´ir a Buga profe” (DC10. MFS.JM21).
CONCLUSIONES
Al iniciar la implementación de la estrategia
didáctica “La granja matemática” producto de la ejecución del proyecto de
intervención “aplicación de las estructuras aditivas
y multiplicativas en
la solución de situaciones problema” en estudiantes de básica primaria (4° y
5°) IE La Magdalena Sede Marco Fidel Suárez en la vereda la Habana de la ciudad
de Buga, se hallaron algunas prevenciones por parte de los estudiantes frente a
la actividad matemática como producto de creencias erróneas formalizadas desde
su experiencia en la escuela y la influencia del contexto familiar y cultural.
Otra posible causa de este hallazgo es la
forma tradicional de aprender y de enseñar matemática, donde se privilegia lo
operacional y la veracidad de los procesos algorítmicos, sin dar lugar a otras
comprensiones del ejercicio matemático. De otro lado, es importante señalar que
las creencias influyen de manera negativa en la disposición anímica y cognitiva
de los estudiantes situación que se evidencia en los siguientes relatos “es que
en mi familia todos somos malos para las matemáticas”. “las matemáticas son muy
aburridas” o “las matemáticas no sirven si no para dolores de cabeza”.
Dentro de las conclusiones más importantes
derivadas a partir de la implementación de esta estrategia, se enuncian las
siguientes:
Se destaca la necesidad de una reflexión
profunda sobre las orientaciones y metodologías empleadas en la enseñanza de
las matemáticas, cuestionando su efectividad y pertinencia en un contexto donde
los estudiantes demandan enfoques más atractivos y personalizados que se
ajusten a sus intereses individuales.
Se identifica una falencia significativa en
la comprensión lectora de los estudiantes en relación con los problemas
matemáticos planteados, lo que sugiere la importancia de fortalecer esta
habilidad como parte integral del proceso educativo en matemáticas.
La propuesta de intervención en el aula
permitió reconocer diversas problemáticas en el enfoque tradicional de la
enseñanza de las matemáticas, destacando la necesidad de adaptarse y actualizar
constantemente las prácticas educativas para satisfacer las demandas y
expectativas de las nuevas generaciones.
Se hace hincapié en la importancia de implementar
estrategias pedagógicas más dinámicas y lúdicas que promuevan un aprendizaje
menos rígido y más motivador en el área de las matemáticas, especialmente en la
educación primaria, donde se sientan las bases del conocimiento matemático.
Se plantea la necesidad de revisar y ajustar
los planes de estudio en matemáticas para incluir enfoques basados en la
resolución de problemas contextualizados y relevantes para la vida cotidiana de
los estudiantes, con el objetivo de fomentar el pensamiento matemático y hacer
que las matemáticas sean más accesibles y significativas para ellos.
REFERENCIAS
Borda, O. F. (1987). Investigación
Participante. Montevideo: Banda Oriental.
Calvo, X. & Salas, N. (2008).
Implementación del enfoque de competencias en la Universidad Estatal a
Distancia. ¿Desafío u oportunidad? En: XIV Congreso Internacional de Tecnología
y Educación a Distancia. UNED. Celebrado en San José, Costa Rica.
Casilimas, C. (2002). Investigación
Cualitativa. Bogotá: ARFO editores e impresores Ltda.
Castro, E. (2004). Desarrollo Del Pensamiento
Matemático Infantil.
Granada: departamento de didactica de las
matemáticas.
Castro,E., Rico, L.,
Castro, E. (1995). Estructuras Aritméticas y Su Modelización. Bogotá: Grupo
Editorial Iberoamérica.
Elliot, J. (1993). El cambio educativo desde
la investigación- acción. Madrid: Morata.
Fraenkel,J. &
Wallen, N. (1996). How to design and evaluate research in education (3𝑟𝑟.Ed.).N ew York: MacGraw-Hill
Gutiérrez, T. D. (2009). Las Matemáticas a Lo
Largo de la Historia: de la Prehistoria a la Antigua Grecia. Madrid: Visión
Libros.
Latorre,
A. (2003). LA INVESTIGACIÓN ACCION.
Conocer y cambiar la práctica
educativa. España: ED. GRAÓ.
Leyva, L., Proenza, Y. (2006). Reflexiones
sobre la calidad del aprendizaje y de las competencias matemáticas. Revista
Iberoamericana de Educación, 40(6), p.12.
Lomax,
P. (1990). Managing
Staff development in
Schools. Clevedon: Multilingual Matters.
Lovell, K. (1962). Desarrollo de los
conceptos básicos matemáticos y científicos en los niños. Madrid: Ediciones
Morata.
Loyes, C. C. (1993). La matemática: creación
y descubrimiento. Madrid: UPCO.
Martínez, P. (2006). El método de estudio de
caso: estrategia metodológica de la investigación científica. Pensamiento y
Gestión,(20) p.167.
Mathiaud, M. (1996). “Enseñar a partir de
actividades”. En: Enseñanza de las matemáticas: matemáticas: relación entre
saberes, programas y prácticas. París: Topiques Editions
Ministerio De Educación Nacional de La
República De Colombia. (2006). Estándares Básicos de Competencia en Matemática.
El porqué de la formación matemática. Bogotá, D.C. Documentos oficiales
Obando, G. y Munera, J. (2003). Las
Situaciones Problema Como Estratégia Para La Conceptualización Matemática.
Revista educación y pedagogía, 15(35), p.185
Pérez, Y., & Ramírez, R. (2011).
Estrategias de enseñanza de la resolución de problemas matemáticos. Fundamentos
teóricos y metodológicos. Scielo Revista de investigación. Caracas,
35(73).p.171
Rico, L. (2006). La competencia matemática en
PISA. PNA, 1(2), 47-66.p.58.
Santos, L. (2007). La resolución de problemas
matemáticos. Fundamentos cognitivos. México: Trillas
Vila, C. y Callejo, M. (2014). Matemáticas
para aprender a pensar, el papel de las creencias en la solución de problemas.
Madrid: Ediciones de la U
ISSN: 2710-088X - ISSN-L: 2710-088X